NN整理
FP:
出自:http://ufldl.stanford.edu/wiki/index.php/Neural_Networks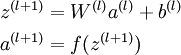
l是当前层数,这里z,W,a,b都是vector。
$a^{(l)}$是本层神经元的输入(其实就是上层神经元的输出)
$W^{(l)}$是上层神经元到本层神经元之间的边上的权值
$b^{(l)}$是本层神经元的bias
$z^{(l+1)}$是本层神经元的上述三者的加权和(实际上是个中间变量)
$f$是激活函数
$a^{(l+1)}$是经过激活函数后本层的输出值
BP:
出自:http://ufldl.stanford.edu/wiki/index.php/Backpropagation_Algorithm
1 残差
对出输出层神经元的残差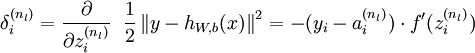
- ${n}_{l}$代表这是第nl层,即最后一层。
- 直观上理解成,先对输出的loss求导,然后乘以激活函数的导数(如果最后一层没有显式的激活函数,那么就当成1为处理)
对于隐层神经元梯度残差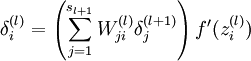
- ${\delta}^{(l)}_{i}$这一层第i个神经元的残差
- ${\delta}^{(l+1)}_{j}$下一层第j个神经元的残差
- ${W}^{l}_{ji}$这一层第i个神经元到下一层第j个神经元之间的权值
- 直观理解成这一层的残差等于它连接成到的下一层的神经元的残差和边上权值的加权和,然后乘上本层的激活函数。
2 梯度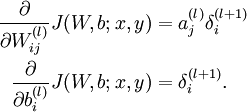
- ${W}^{(l)}_{ij}$第l层神经元第i个神经元到第l+1层第j个神经元边上的权值
- ${a}^{(l)}_{j}$第l层神经元的第j个神经元的输出
- ${\delta}^{(l+1)}_{i}$第l+1层第i个神经元的误差
- 也就是,一条边上的权值的梯度,为左边神经元的输出乘以右边神经元误差的值。



