关于卷积

20150211

感觉从学习高数开始就没有搞明白过卷积究竟是干嘛的，google了一下有什么比较直观的理解方式，得到的大都与时域和信号有关（比如这篇,这篇），其实我想搞明白的是卷积跟图像处理的关系(这篇提到一点)。先记录一些目前似懂非懂的内容。

卷积 vs 互相关
从知乎一个帖子拷贝过来的：两个函数，翻转其中一个，再滑动求积分，叫卷积（convultion）；不翻转就滑动求积分，叫做互相关（cross-correlation，有时候简写为correlation）。如果其中之一是偶函数，那么卷积和互相关效果相同。

这里算的互相关在图像中就是很平常的滤波运算。(这里说的有点歧义，因为也有convolution filter这个说法，filter如果翻译成滤波器的话，那么“滤波”具有更加广的含义，只要符合“过滤掉某种频率的波形”的作用的kernel应该都可以称为滤波器，不管它是卷积还是相关的)

用matlab验证一下确实如此，互相关对应的是filter2，卷积对应的是conv2。（注意到matlab中还有filter和conv函数，应该是带2的是2维操作，不带2的是一维操作）

a = [1 2;3 4;5 6];
b = [1 2;3 4];
% 下面两个是等价的运算，其实filter2函数是调用conv2函数来实现的
filter2(b, a, 'valid');
conv2(a, rot90(b, 2), 'valid'); %这里的rot90(b, 2)对应了“翻转”的操作，即旋转180度

20150216

今天又查了一下卷积跟互相关的关系，从这里得到一些有趣的信息。

1. Correlation is measuring how similar two signals are to each other, and convolution is directly related to the impulse response
2. Correlation is the degree of similarity between two different signals not convolution. Convolution is the product of two signals in frequency domain.

上面第二点中提到卷积是信号在频域上的乘积（也就是卷积定理），这里就涉及到了傅里叶变换了。知乎上有一篇文章做了比较直观的解释，也先记录在这里，copy几个有意思的图：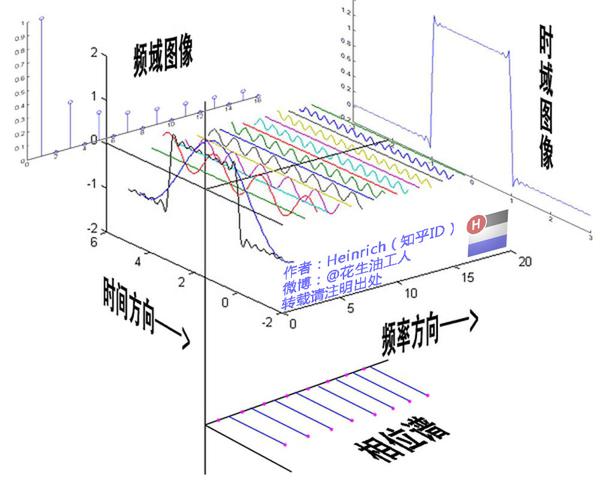

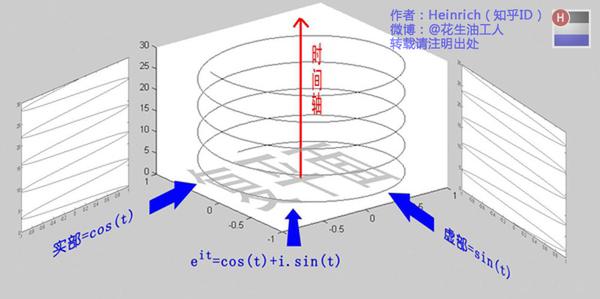
20150217

虽然看了一些资料，但是感觉一些疑问还是没有得到解决

1. 如果“卷积=旋转180度的相关运算”的说法成立，那么为何在图像说的一般的sobel算子等是卷积运算呢？
2. 在CNN中可视化卷积核有什么意义呢？就是看他长得像什么，就说是什么？感觉不太合理的样子。

然后今天又看了一个跟问题1有关的帖子：
http://dsp.stackexchange.com/questions/12684/difference-between-correlation-and-convolution-on-an-image
这里答主说为何要用卷积而不是相关，是因为卷积是频域上的乘积，是满足结合律的。所以，如果对于图像f，依次用g和h去卷的话，其实等价于用g和h卷出一个核，然后用这个核去卷f。如果按照这个说法，CNN其实也是可以这样卷的咯？如果先将不同的核都先结合起来，最后再去卷图像，这样运算效率会变高吗？
感觉问题反而是变多了，看来本人的基础不够扎实才是命门所在啊。。